理想极化电极与界面参数
理想极化电极 (IPE) 是研究电极/溶液界面结构和性质的理论前提。它被定义为在研究电位范围内不发生任何电极反应的电化学体系。
$R_f \to \infty$
此时,通过电极的所有电流都用于改变界面电荷和电位,其等效电路是一个纯电容 $C$。
在 IPE 体系中,界面的状态可以由三个核心参数随电极电位 $\phi$ 变化的函数关系来描述:
- 界面张力 $\sigma$
- 表面剩余电荷密度 $q$
- 微分电容 $C_d$
Lippmann 公式与零电荷电位
研究界面性质首先需要建立热力学关系,即 Lippmann 公式。它将宏观可测量的界面张力 $\sigma$ 与界面的电荷状态 $q$ 联系起来。
根据 Gibbs 等温吸附方程(忽略化学反应和组分变化):
$$\text{d}\sigma = - \sum \Gamma_i \text{d}\mu_i$$
对于 IPE,溶液相组分 $\mu_i$ 不变 ($\text{d}\mu_i=0$),但考虑到电极上的电子吸附(即 $q$ 的存在):
$$\text{d}\sigma = - \Gamma_e \text{d}\mu_e$$
其中,电子的表面吸附量 $\Gamma_e$ 与表面电荷密度 $q$ 的关系为 $\Gamma_e = -q/F$,电子化学位变化 $\text{d}\mu_e$ 与电极电位 $\phi$ 的关系为 $\text{d}\mu_e = -F\text{d}\phi$。代入并简化可得著名的 Lippmann 公式:
$$\left(\frac{\partial \sigma}{\partial \phi}\right)_{\text{T}, \text{p}, \mu_i} = -q$$
该公式是连接宏观测量(电毛细曲线的斜率)和界面微观状态(表面电荷密度)的桥梁。
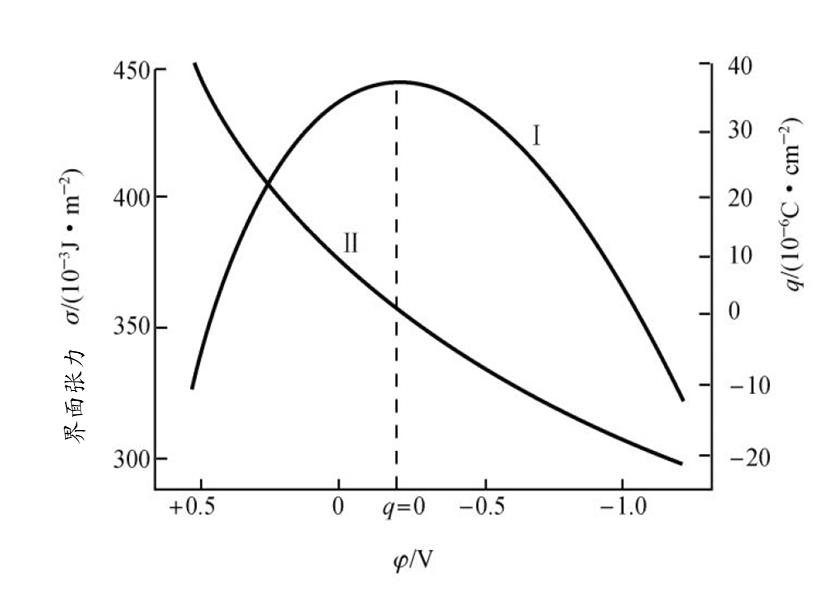
汞电极的电毛细曲线与表面剩余电荷密度-电位曲线
零电荷电位 ($\phi_0$) 的概念正是由 Lippmann 公式导出:
当界面张力 $\sigma$ 达到最大值时,其微分值 $\left(\frac{\partial \sigma}{\partial \phi}\right)$ 为零。
$$\left(\frac{\partial \sigma}{\partial \phi}\right)_{\phi=\phi_0} = 0$$
此时,电极表面剩余电荷密度 $q$ 为零,该电位即为 $\phi_0$。
微分电容与积分电容
微分电容 $C_d$ 定义为表面电荷密度 $q$ 对电极电位 $\phi$ 的一阶导数,表征了界面储存电荷的能力:
$$C_d = \left(\frac{\partial q}{\partial \phi}\right)_{\text{T}, \text{p}, \mu_i}$$
微分电容 $C_d$ 与界面张力 $\sigma$ 的关系,即 $C_d$ 是 $\sigma$ 对 $\phi$ 的二阶微分:
$$C_d = -\left(\frac{\partial^2 \sigma}{\partial \phi^2}\right)_{\text{T}, \text{p}, \mu_i}$$
积分电容 $C_i$ 定义为从零电荷电位 $\phi_0$ 到某一电位 $\phi$ 之间的平均电容:
$$C_i = \frac{q}{\phi - \phi_0} = \frac{1}{\phi - \phi_0} \int_{\phi_0}^{\phi} C_d \text{d}\phi$$
微分电容法与电毛细曲线法的对比
根据上述关系,微分电容 $C_d$ 是 $q$ 的微分函数,而 $q$ 是 $\sigma$ 的微分函数,$\sigma$ 是 $q$ 的积分函数。
$C_d$ 是 $\sigma$ 的二阶微分。
微分函数比积分函数更灵敏地反映原函数的细微变化。因此,通过 微分电容法 测量 $C_d$ 进而计算 $q$ ($q = \int C_d \text{d}\phi$) 比通过 电毛细曲线法 测量 $\sigma$ 进而计算 $q$ ($q = -\text{d}\sigma/\text{d}\phi$) 更精确、更灵敏。
双电层模型定量推导与对比
双电层模型从平板电容器模型(Helmholtz)发展到考虑热运动影响的分散层模型(Gouy-Chapman),最终到 Stern 模型,形成了紧密层和分散层串联的基本结构。
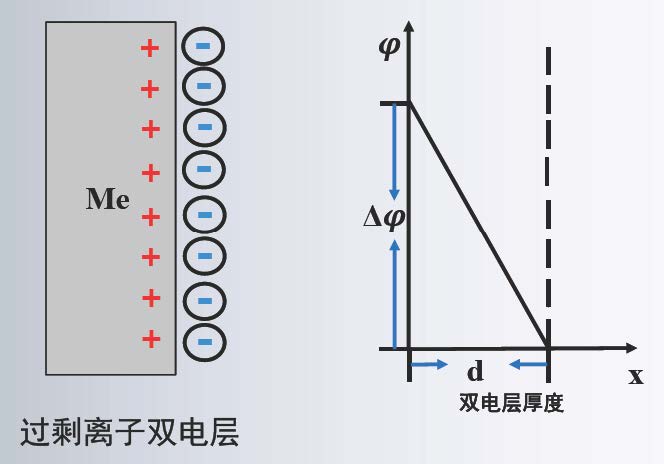
1. Helmholtz (H) 模型(紧密层模型)
紧密层模型示意图
将双电层简化为平行板电容器,忽略热运动和电位在紧密层内的非均匀性。
$$C_{\text{H}} = \frac{\epsilon_0 \epsilon_r}{l}$$
其中,$\epsilon_0$ 是真空介电常数,$\epsilon_r$ 是相对介电常数,$l$ 是电荷层间距(紧密层厚度 $d$)。
该模型预测电容 $C_{\text{H}}$ 为恒定值,无法解释 $C_d$ 随 $\phi$ 变化和稀溶液中 $C_d$ 出现最小值的实验事实。
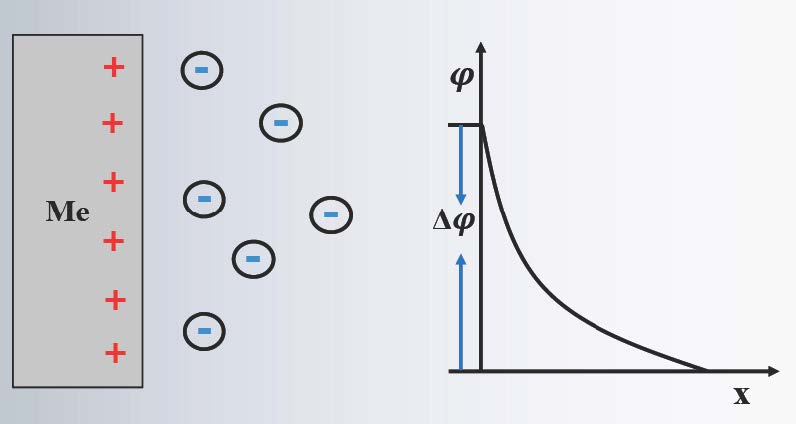
2. Gouy-Chapman (G-C) 模型(分散层模型)
分散层模型示意图
该模型考虑了离子热运动,认为溶液侧电荷是分散分布的。基于 Poisson 方程和Boltzmann 分布推导出离子浓度 $c_i$ 随电位 $\psi$ 变化的定量关系,进而导出分散层电容 $C_{\text{分}}$ 和德拜长度 $l$。
对于 $\text{z-z}$ 价型电解质(如 $\text{KCl}$),在电荷密度 $q$ 和溶液浓度 $c$ 均很小,即 $|z \psi_1 F| \ll RT$ 时,分散层电容 $C_{\text{分}}$ 约等于整个双电层电容 $C_d$。此时可将 $\text{G-C}$ 模型中的双曲正弦函数按泰勒级数展开,并与平行板电容器公式进行比较。
从 G-C 方程式(当 $|z \psi_1 F| \ll RT$):
$$q \approx \sqrt{\frac{2 c \epsilon_0 \epsilon_r}{RT}} z F \psi_1$$
分散层电容 $C_{\text{分}}$ 为 $C_{\text{分}} = \text{d}q / \text{d}\psi_1$:
$$C_{\text{分}} = \sqrt{\frac{2 c \epsilon_0 \epsilon_r}{RT}} z F$$
将 $C_{\text{分}}$ 形式与 $C_{\text{H}} = \epsilon_0 \epsilon_r / l$ 形式进行对比,可得出德拜长度 $l$(分散层有效厚度):
$$l = \frac{RT}{z F} \sqrt{\frac{\epsilon_0 \epsilon_r}{2 c}}$$
概念理解与对比:
- 德拜长度 $l$ 代表了分散层中剩余电荷分布的有效范围。
- $l$ 与浓度的关系:$l \propto 1/\sqrt{c}$,即溶液浓度 $c$ 增大,德拜长度 $l$ 减小(分散层被压缩)。
- $C_{\text{分}}$ 与浓度的关系:$C_{\text{分}} \propto \sqrt{c}$,即浓度 $c$ 增大,分散层电容 $C_{\text{分}}$ 增大。
- G-C 模型的成功:解释了 $C_d$ 随 $c$ 增大而增大,解释了稀溶液中 $C_d$ 出现最小值(因为此时 $\psi_1 \to 0$,G-C 预测 $C_{\text{分}} \to 0$)。
- G-C 模型的不足:完全忽略了紧密层,无法解释浓溶液中 $C_d$ 出现平台区。
3. Stern 模型(紧密层与分散层串联)
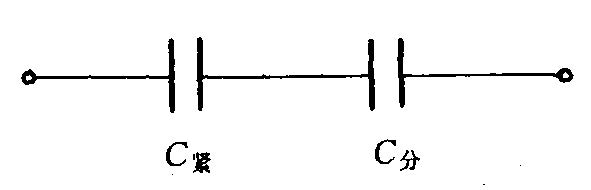
双电层微分电容由紧密层电容和分散层电容串联组成
Stern 模型将 G-C 模型和 H 模型结合,认为总电容 $C_d$ 是紧密层电容 $C_{\text{紧}}$ 和分散层电容 $C_{\text{分}}$ 的串联。
$$\frac{1}{C_d} = \frac{1}{C_{\text{紧}}} + \frac{1}{C_{\text{分}}}$$
斯特恩模型的成功在于:
解释 $C_d$ 随 $c$ 变化:
- 稀溶液:$C_{\text{分}}$ 很小,根据串联关系 $C_d \approx C_{\text{分}}$。此时 $C_d$ 对浓度敏感,并出现最小值。
- 浓溶液:$C_{\text{分}}$ 很大(德拜长度 $l$ 很小),根据串联关系 $C_d \approx C_{\text{紧}}$。此时 $C_d$ 趋于恒定值,出现平台区。
离子和有机物特性吸附对界面性质的影响
特性吸附是电极和溶液中粒子之间的短程相互作用(非静电作用)的结果。
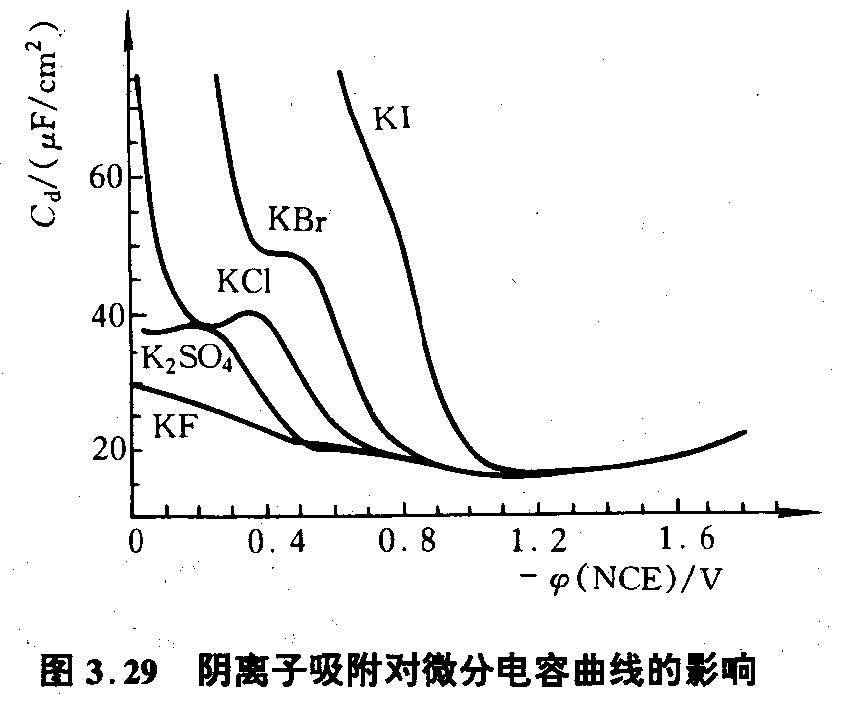
阴离子吸附对微分电容影响
| 活性物 | 对 $\phi_0$ 的影响 | 对 $C_d$ 的影响 | 紧密层结构变化 | 关键机制 |
|---|---|---|---|---|
| 阴离子($\text{Cl}^-, \text{Br}^-, \text{I}^-$ 等) | $\phi_0$ 向负电位移动 | 在比 $\phi_0$ 更正电位处 $C_d$ 升高 | 形成内紧密层 (IHP),阴离子脱去水化膜,直接吸附。厚度 $d$ 减小。 | 阴离子在正电荷电极表面超载吸附,$d$ 减小,增强 $C_{\text{紧}}$。 |
| 阳离子(少数 $\text{Tl}^+, \text{Cs}^+$) | $\phi_0$ 向正电位移动 | $C_d$ 升高 | 无特性吸附时形成外紧密层 (OHP),由水偶极层和水化阳离子层串联。$C_{\text{紧}}$ 仅取决于水偶极层。 |
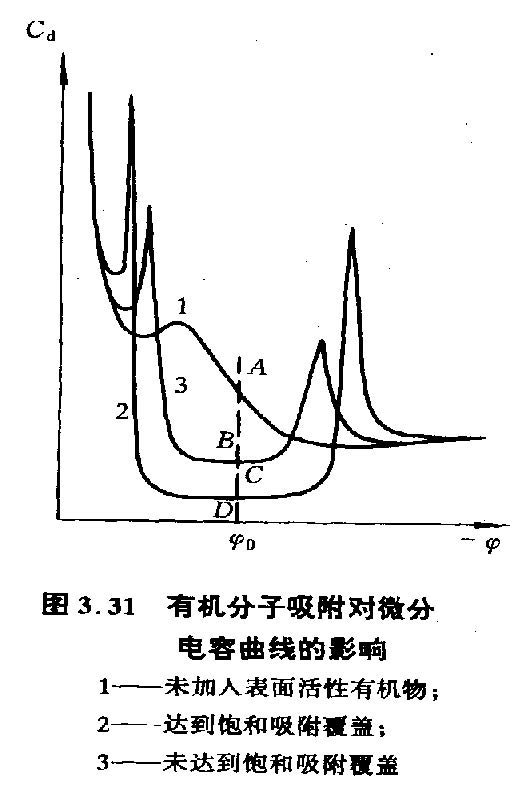
有机分子吸附对微分电容曲线的影响
| 活性物 | 对 $\phi_0$ 的影响 | 对 $C_d$ 的影响 | 紧密层结构变化 | 关键机制 |
|---|---|---|---|---|
| 有机分子 | $\phi_0$ 向正或负移动 | $\phi_0$ 附近 $C_d$ 下降,两侧有峰 | 取代水偶极层,形成吸附偶极子层。 | 有机分子 $\epsilon_r$ 小,$l$ 大,导致 $C_d$ 减小,吸脱附峰对应吸附覆盖度 $\theta$ 变化剧烈。 |
氢氧吸附与电位扫描法
氢和氧在 Pt 等催化电极表面的吸附伴随着电化学反应,因此该体系不是理想极化电极,不能用 $C_d$ 或 $\sigma$ 研究。
研究方法:充电曲线法或电位扫描法(循环伏安法)。
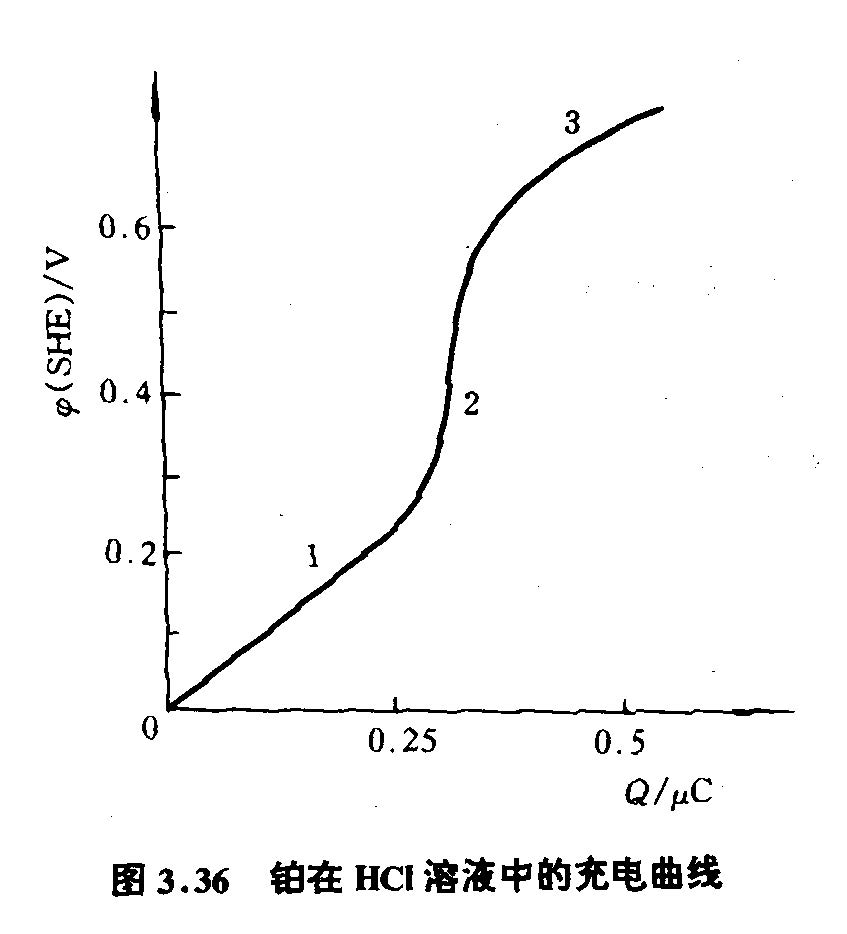
铂电极在HCl溶液中的充电曲线
| 名称 | 核心概念 | 图像识别与认知 | 概念深化与归纳 |
|---|---|---|---|
| 铂在 $\text{HCl}$ 溶液中的充电曲线 | 氢氧吸附研究方法、三区划分 | 第一段(氢吸附区):$\phi \to 0$。斜率小($C_d$ 极大),电量用于吸附氢氧化。 第二段(双电层区):斜率大($C_d$ 小),电量用于双电层充电。 第三段(氧吸附区):$\phi$ 更正。斜率小($C_d$ 增大),电量用于氧吸附。 | 充电曲线法通过 $\text{d}\phi/\text{d}Q$ 的斜率计算 $C_d$。三区划分反映了不同电位下界面发生的主要过程。 |
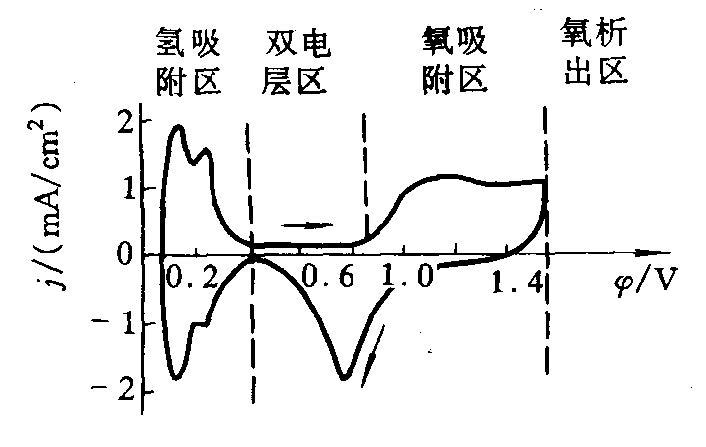
铂电极在2.3mol/L硫酸溶液中的伏安循环曲线
| 曲线区域 | 对应过程 | 过程特性 | 概念联系 |
|---|---|---|---|
| 最负电位区 | 氢吸附/脱附峰 | 可逆(峰位几乎重合) | 氢原子以化学吸附态存在,吸附是有选择性的。 |
| 中间平台区 | 双电层充电 | 无电化学反应 | 电流 $j$ 最小,对应于双电层区的充电电流。 |
| 最正电位区 | 氧吸附/脱附峰 | 不可逆(吸附和脱附峰位差大,有滞后环) | 氧吸附导致钝化,使电极反应活化能增大,反应速率降低。 |
作者:GARFIELDTOM
邮箱:coolerxde@gt.ac.cn