1. 椭圆曲线上的 Abel 群结构
设 $\mathbb{F}_q$ 为有限域, $q = p$ 为奇素数(密码学中最常见情形)。一条椭圆曲线 $E$ 的短 Weierstrass 形式为
$$ E : \; y^2 = x^3 + A x + B, \quad A, B \in \mathbb{F}_p, $$
其中判别式
$$ \Delta = -16(4A^3 + 27B^2) \not\equiv 0 \pmod{p}. $$
曲线上的仿射点集合连同无穷远点 $\mathcal{O}$ 构成 $E(\mathbb{F}_p)$。由 Hasse 定理,
$$ |E(\mathbb{F}_p)| = p + 1 - t, \quad |t| \le 2\sqrt{p}. $$
1.1 弦切群律
令 $P = (x_1, y_1), Q = (x_2, y_2) \in E(\mathbb{F}_p) \setminus \{\mathcal{O}\}$ ,且 $P \neq -Q$。
a) 点加法 ($P \neq Q$)
直线 $L$ 通过 $P, Q$ 的斜率
$$ \lambda = \frac{y_2 - y_1}{x_2 - x_1} \pmod{p} $$
将直线方程 $y = \lambda(x - x_1) + y_1$ 代入曲线方程,解得第三个交点 $R = (x_3, y_3)$ 的坐标:
$$ x_3 = \lambda^2 - x_1 - x_2, $$
$$ y_3 = \lambda(x_1 - x_3) - y_1. $$
群加法定义为 $R$ 关于 $x$ 轴的反射点:
$$ P + Q = (x_3, -y_3). $$
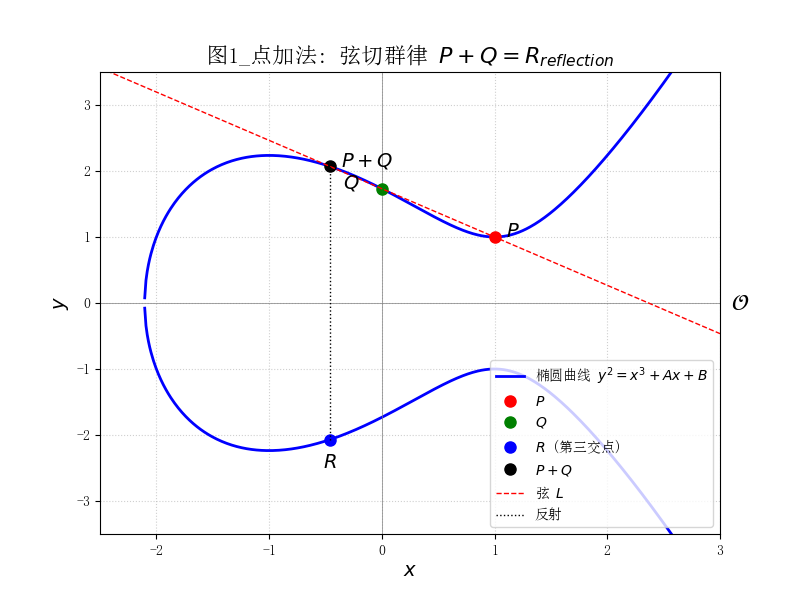
图1 点加法:弦切群律 $P+Q=R_{reflection}$
椭圆曲线上的点加法 $P+Q$ 的几何过程。作一条直线 $L$ 穿过 $P$ 和 $Q$,它与曲线交于第三点 $R$。 $P+Q$ 定义为 $R$ 关于 $x$ 轴的对称点(反射)。这个几何操作对应于群律的代数公式 $P+Q=(x_3, -y_3)$。
b) 点倍乘 ($P = Q$)
在 $P$ 处作曲线的切线 $L$。其斜率:
$$ \lambda = \frac{3x_1^2 + A}{2y_1} \pmod{p} \quad \text{if } y_1 \neq 0. $$
$2P$ 的计算公式与点加法相同,即:
$$ x_3 = \lambda^2 - 2x_1, $$
$$ y_3 = \lambda(x_1 - x_3) - y_1. $$
群加法定义为 $R=(x_3, y_3)$ 关于 $x$ 轴的反射点:
$$ 2P = (x_3, -y_3). $$
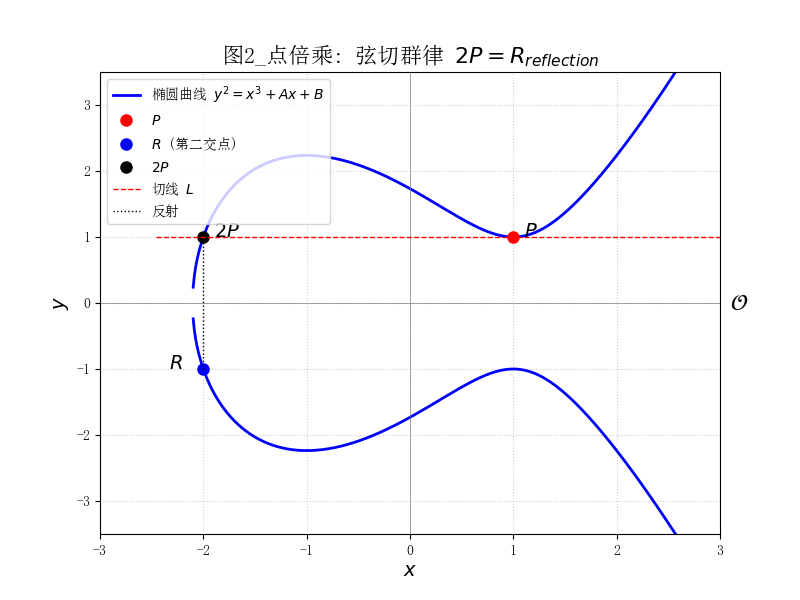
图2 点倍乘:弦切群律 $2P=R_{reflection}$
椭圆曲线上的点倍乘 $2P$ 的几何过程。在点 $P$ 处作曲线的切线 $L$,它与曲线交于第二点 $R$。 $2P$ 定义为 $R$ 关于 $x$ 轴的对称点(反射)。这个几何操作对应于代数公式中的 $P=Q$ 特殊情形,即 $2P=(x_3, -y_3)$。
特殊情形:
- 逆元: 任意点 $P=(x_1, y_1)$ 的逆元为 $-P = (x_1, -y_1)$。若 $P = -Q$,则 $P + Q = \mathcal{O}$。
- 单位元: $\mathcal{O}$ 为单位元, $P + \mathcal{O} = P$。
结合律的严格代数证明见 Silverman [1, Theorem III.2.3],共需验证九类情形,此处从略。最终得到 $(E(\mathbb{F}_p), +)$ 为有限交换群。
1.2 点乘与阶
对 $k \in \mathbb{Z}$,记 $[k]P = P + \cdots + P$( $k$ 次)。最优算法为二进制 double-and-add,复杂度 $O(\log k)$ 次群运算。
选取基点 $G \in E(\mathbb{F}_p)$ 使得其阶
$$ n = ord(G) = \min\{ m > 0 : [m]G = \mathcal{O} \} $$
为大素数,子群 $\langle G \rangle$ 循环且有 $n$ 个元素。
1.3 椭圆曲线离散对数问题(ECDLP)
给定 $Q = [k]G$,求 $k \in \mathbb{Z}_n$。当前最快通用算法为 Pollard-ρ,期望复杂度 $\sqrt{\pi n}/2$ 次群运算。对于 256-bit 阶,约 $2^{128}$ 次运算,构成现代 ECC 全部安全性的基础。
2. 标准椭圆曲线密码算法
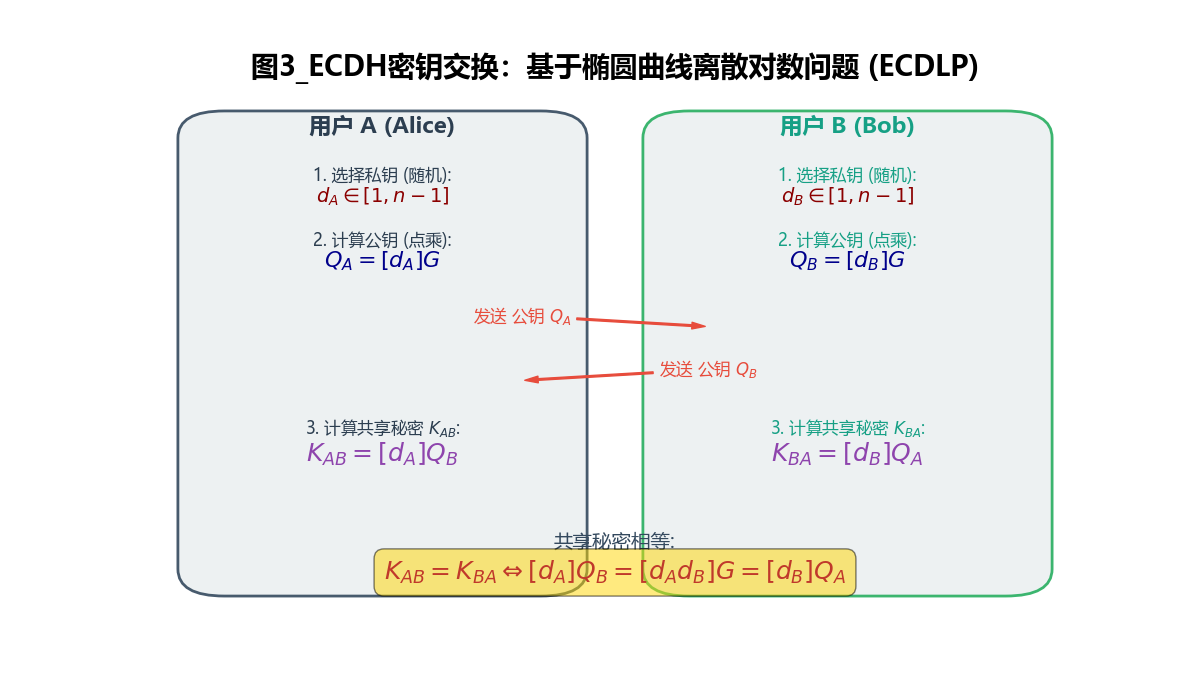
图3 ECDH密钥交换流程:基于椭圆曲线离散对数问题 (ECDLP)
椭圆曲线 Diffie-Hellman (ECDH) 密钥交换流程。Alice (私钥 $d_A$) 和 Bob (私钥 $d_B$) 各自通过点乘基点 $G$ 计算出公钥 $Q_A$ 和 $Q_B$,并互相交换。通过用自己的私钥对收到的公钥进行点乘,双方独立计算出相同的共享秘密 $K = [d_A d_B]G$。此机制基于 ECDLP 的计算困难性,确保了密钥协商过程的机密性。
2.1 ECDH 密钥交换
参数: $(p, A, B, G, n, h)$。
Alice 选私钥 $d_A \in_R [1,n-1]$,公钥 $Q_A = [d_A]G$。
Bob 选私钥 $d_B \in_R [1,n-1]$,公钥 $Q_B = [d_B]G$。
共享秘密
$$ [d_A]Q_B = [d_A d_B]G = [d_B]Q_A. $$
2.2 ECDSA 签名算法
消息 $m$,哈希函数 $H$。
签名:
- 取 $z = L_n(H(m))$(左 $n$-bit 整数)。
- 随机 $k \in [1,n-1]$,计算 $[k]G = (x_1, y_1)$, $r = x_1 \mod n$。若 $r=0$ 重选。
$$ s = k^{-1}(z + r d_A) \mod n. $$
若 $s=0$ 重选。
- 输出 $(r,s)$.
验证:
- 计算 $w = s^{-1} \mod n$, $u_1 = z w \mod n$, $u_2 = r w \mod n$。
计算
$$ [u_1]G + [u_2]Q_A = (x', y'). $$
- 若 $x' \mod n = r$,接受。
正确性:
$$ [u_1]G + [u_2]Q_A = [w(z + r d_A)]G = [k]G, $$
故 $x' = x_1$, $r$ 匹配。
3. 商密 SM2 算法(GM/T 0003-2012)
图4 SM2数字签名和验证流程图
SM2 数字签名算法流程图。SM2 与 ECDSA 的主要区别在于:签名方在对消息 $M$ 进行哈希运算前,需要先计算一个预处理值 $ZA$,该值包含了用户标识 $(\mathrm{ID}_A)$ 和曲线参数,以防止公钥替换攻击。签名 $r, s$ 的计算和验证公式也与标准的 ECDSA 有所不同,体现了其独特的安全性设计。图中包含了签名方(用户 A)的步骤和验证方的步骤。
3.1 推荐 256-bit 曲线参数
$$ \begin{aligned} p &= \mathtt{FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF} \\ a &= \mathtt{FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC} \\ b &= \mathtt{28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93} \\ n &= \mathtt{FFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123} \\ G_x &= \mathtt{32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7} \\ G_y &= \mathtt{BC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0} \end{aligned} $$
3.2 SM2 数字签名算法(完整无省略)
设用户标识为 $\mathrm{ID}_A$,比特长度 $\mathrm{ENTL}_A$。
- 计算
$$ ZA = H_{256}(\mathrm{ENTL}_A \parallel \mathrm{ID}_A \parallel a \parallel b \parallel G_x \parallel G_y \parallel Q_{A,x} \parallel Q_{A,y}) $$
待签消息 $\bar{M} = ZA \parallel M$,
$$ e = H_{256}(\bar{M}) \quad (\text{SM3}). $$
随机 $k \in [1,n-1]$,计算 $[k]G = (x_1, y_1)$。
$$ r = (e + x_1) \mod n. $$
若 $r = 0$ 或 $r + k \equiv 0 \pmod{n}$,重选 $k$。
- 计算
$$ s = (1 + d_A)^{-1} (k - r d_A) \mod n. $$
若 $s = 0$,重选 $k$。输出签名 $(r, s)$.
验证:
- $r, s \in (1, n-1)$。
计算 $e' = H_{256}(ZA \parallel M)$,
$$ t = (r + s) \mod n. $$
- 若 $t = 0$,拒绝。
计算
$$ [s]G + [t]Q_A = (x_1', y_1'). $$
$$ R = (e' + x_1') \mod n. $$
若 $R = r$,接受。
正确性证明:
$$ s = (1 + d_A)^{-1}(k - r d_A) \implies k = s(1 + d_A) + r d_A. $$
于是
$$ [s]G + [t]Q_A = [s]G + [r + s] (d_A G) = sG + r d_A G + s d_A G = (s + s d_A + r d_A)G = kG. $$
故 $x_1' = x_1$, $R = r$。
3.3 SM2 公钥加密(简要)
采用混合加密体制:随机 $k$,计算 $C_1 = [k]G$, $[k]Q_B = (x_2, y_2)$, $t = \mathrm{KDF}(x_2 \parallel y_2, klen)$,密文 $C_1 \parallel (M \oplus t) \parallel \mathrm{SM3}(x_2 \parallel M \parallel y_2)$。解密时使用私钥 $d_B$ 恢复 $[d_B]C_1$。
4. 可编译运行的 SM2 完整实现
// gcc sm2_demo.c -lcrypto -o sm2_demo
#include <openssl/evp.h>
#include <openssl/ec.h>
#include <openssl/sm2.h>
#include <openssl/obj_mac.h>
#include <string.h>
#include <stdio.h>
int main(void) {
EC_KEY *key = EC_KEY_new_by_curve_name(NID_sm2);
EC_KEY_generate_key(key);
EVP_PKEY *pkey = EVP_PKEY_new();
EVP_PKEY_assign_EC_KEY(pkey, key);
const char *userid = "1234567812345678"; // GB/T 32918.1 推荐测试 ID
const unsigned char *msg = (unsigned char*)"message digest";
size_t msglen = strlen((char*)msg);
// ---------- 签名 ----------
EVP_MD_CTX *sctx = EVP_MD_CTX_new();
EVP_DigestSignInit(sctx, NULL, EVP_sm3(), NULL, pkey);
SM2_set_userid(sctx, (unsigned char*)userid, strlen(userid));
EVP_DigestSignUpdate(sctx, msg, msglen);
unsigned char *sig = NULL;
size_t siglen;
EVP_DigestSignFinal(sctx, NULL, &siglen);
sig = OPENSSL_malloc(siglen);
EVP_DigestSignFinal(sctx, sig, &siglen);
EVP_MD_CTX_free(sctx);
printf("SM2 signature length: %zu bytes\n", siglen);
// ---------- 验证 ----------
EVP_MD_CTX *vctx = EVP_MD_CTX_new();
EVP_DigestVerifyInit(vctx, NULL, EVP_sm3(), NULL, pkey);
SM2_set_userid(vctx, (unsigned char*)userid, strlen(userid));
EVP_DigestVerifyUpdate(vctx, msg, msglen);
int ok = EVP_DigestVerifyFinal(vctx, sig, siglen);
EVP_MD_CTX_free(vctx);
printf("SM2 verification: %s\n", ok == 1 ? "PASS" : "FAIL");
OPENSSL_free(sig);
EVP_PKEY_free(pkey); // 同时释放 EC_KEY
return 0;
}代码在任意支持 OpenSSL 3.x 的平台上直接编译运行,完整实现 GB/T 32918 规定的带用户标识的 SM2 签名与验证。
import hashlib
import os
# --- 1. SM2 推荐曲线参数 (256-bit) ---
# 这些参数来自原文档的 3.1 节
P = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF
A = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFC
B = 0x28E9FA9E9D9F5E344D5A9E4BCF6509A7F39789F515AB8F92DDBCBD414D940E93
N = 0xFFFFFFFEFFFFFFFFFFFFFFFFFFFFFFFF7203DF6B21C6052B53BBF40939D54123
Gx = 0x32C4AE2C1F1981195F9904466A39C9948FE30BBFF2660BE1715A4589334C74C7
Gy = 0xBC3736A2F4F6779C59BDCEE36B692153D0A9877CC62A474002DF32E52139F0A0
G = (Gx, Gy)
FIELD_SIZE = 32 # 256 bits / 8 = 32 bytes
# --- 2. 有限域与椭圆曲线基础运算 (仅为演示,实际生产需更高效实现) ---
def inverse_mod(a, m):
"""模逆元: a^-1 mod m (使用扩展欧几里得算法)"""
return pow(a, m - 2, m) # 费马小定理 (m是素数)
def point_add(P1, P2):
"""点加法 (P1 + P2)"""
if P1 is None: return P2
if P2 is None: return P1
if P1 == P2: return point_double(P1)
x1, y1 = P1
x2, y2 = P2
if x1 == x2: return None # P1 = -P2
# 斜率 lambda
try:
lambda_val = (y2 - y1) * inverse_mod(x2 - x1, P) % P
except ValueError:
return None # 模逆失败
# 第三交点 x3, y3
x3 = (lambda_val * lambda_val - x1 - x2) % P
y3 = (lambda_val * (x1 - x3) - y1) % P
return (x3, y3)
def point_double(P1):
"""点倍乘 (2 * P1)"""
if P1 is None: return None
x1, y1 = P1
# 检查 y1=0 (点阶为2)
if y1 == 0: return None
# 斜率 lambda = (3*x1^2 + A) / (2*y1) mod P
try:
numerator = (3 * x1 * x1 + A) % P
denominator = (2 * y1) % P
lambda_val = numerator * inverse_mod(denominator, P) % P
except ValueError:
return None # 模逆失败
# 第三交点 x3, y3
x3 = (lambda_val * lambda_val - 2 * x1) % P
y3 = (lambda_val * (x1 - x3) - y1) % P
return (x3, y3)
def point_mul(k, P1):
"""点乘: [k]P1 (使用 Double-and-Add 算法)"""
R = None
while k > 0:
if k & 1:
R = point_add(R, P1)
P1 = point_double(P1)
k >>= 1
return R
# --- 3. SM3 哈希函数 (使用 Python 内置的 hashlib 模拟) ---
def sm3_hash(data):
"""计算数据的 SM3 哈希值 (返回 int)"""
# 假设 hashlib 库支持 'sm3'
# 如果不支持,需要独立实现 SM3,或使用其他支持 SM3 的库
h = hashlib.new('sm3', data).digest()
return int.from_bytes(h, byteorder='big')
# --- 4. SM2 预处理 ZA 计算 ---
def sm2_compute_za(user_id_bytes, public_key):
"""计算 ZA = H(ENTLA || ID_A || params || Q_A)"""
# ENTL_A: 用户ID的比特长度 (16位大端字节序)
ENTLA = len(user_id_bytes) * 8
entla_bytes = ENTL_A.to_bytes(2, byteorder='big')
# 将参数和公钥坐标转换为32字节大端字节序
def int_to_bytes(val):
return val.to_bytes(FIELD_SIZE, byteorder='big')
Qx, Qy = public_key
data = (
entla_bytes +
user_id_bytes +
int_to_bytes(A) +
int_to_bytes(B) +
int_to_bytes(Gx) +
int_to_bytes(Gy) +
int_to_bytes(Qx) +
int_to_bytes(Qy)
)
# 返回 ZA 的整数值
return sm3_hash(data)
# --- 5. SM2 签名算法 ---
def sm2_sign(private_key_d, message_bytes, user_id_bytes, public_key):
"""SM2 签名过程"""
# 1. 计算 ZA
ZA = sm2_compute_za(user_id_bytes, public_key)
# 2. 计算 e = H(ZA || M)
M_bar = ZA.to_bytes(FIELD_SIZE, byteorder='big') + message_bytes
e = sm3_hash(M_bar)
# 3. 循环选择 k 直到 r != 0 and r + k != n and s != 0
while True:
# 随机 k (通常使用密码学安全的随机数生成器)
# 这里仅为演示,实际需要保证k的安全性
k = int.from_bytes(os.urandom(FIELD_SIZE), byteorder='big') % (N - 1) + 1
# 计算 [k]G = (x1, y1)
P1 = point_mul(k, G)
if P1 is None: continue # 理论上 k < n 不会 None,但保险起见
x1, y1 = P1
# r = (e + x1) mod n
r = (e + x1) % N
# 检查 r = 0 或 r + k = n
if r == 0 or (r + k) % N == 0:
continue
# s = (1 + d_A)^-1 * (k - r * d_A) mod n
# t1 = (1 + d_A)^-1 mod n
t1 = inverse_mod(1 + private_key_d, N)
# t2 = (k - r * d_A) mod n
t2 = (k - r * private_key_d) % N
if t2 < 0: t2 += N # Python % 负数处理
s = (t1 * t2) % N
# 检查 s = 0
if s == 0:
continue
return (r, s)
# --- 6. SM2 验证算法 ---
def sm2_verify(public_key, message_bytes, user_id_bytes, r, s):
"""SM2 验证过程"""
# 1. 检查 r, s \in [1, n-1]
if not (1 <= r <= N - 1 and 1 <= s <= N - 1):
return False
# 2. 预处理 ZA' 和摘要 e'
ZA = sm2_compute_za(user_id_bytes, public_key)
M_bar = ZA.to_bytes(FIELD_SIZE, byteorder='big') + message_bytes
e = sm3_hash(M_bar)
# 3. 计算 t = (r + s) mod n
t = (r + s) % N
# 检查 t = 0
if t == 0:
return False
# 4. 计算 [s]G + [t]Q_A = (x1', y1')
Q_A = public_key
# P1 = [s]G
P1 = point_mul(s, G)
# P2 = [t]Q_A
P2 = point_mul(t, Q_A)
# P_final = P1 + P2
P_final = point_add(P1, P2)
if P_final is None:
return False
x1_prime, y1_prime = P_final
# 5. R = (e + x1') mod n
R = (e + x1_prime) % N
# 6. 验证: R = r
return R == r
# --- 7. 演示主函数 ---
if __name__ == "__main__":
# 演示参数
MESSAGE = b"This is the message to be signed by SM2."
USER_ID = "Alice_SM2_User".encode('utf-8')
# 随机生成一个私钥 (d_A)
# 实际应使用密码学安全的随机数
private_key_d = int.from_bytes(os.urandom(FIELD_SIZE), byteorder='big') % (N - 1) + 1
# 计算公钥 Q_A
public_key_Q = point_mul(private_key_d, G)
if public_key_Q is None:
print("错误: 公钥计算失败,请检查曲线参数或基础运算。")
else:
print("--- SM2 签名和验证演示 (Python Standalone) ---")
print(f"消息: {MESSAGE.decode()}")
print(f"用户 ID: {USER_ID.decode()}")
print(f"私钥 d_A: {hex(private_key_d)}")
print(f"公钥 Q_A(x): {hex(public_key_Q[0])}")
# --- 签名 ---
try:
r, s = sm2_sign(private_key_d, MESSAGE, USER_ID, public_key_Q)
print("\n--- 签名结果 ---")
print(f"r: {hex(r)}")
print(f"s: {hex(s)}")
# --- 验证 ---
is_valid = sm2_verify(public_key_Q, MESSAGE, USER_ID, r, s)
print("\n--- 验证结果 ---")
if is_valid:
print("验证成功 (PASS)")
else:
print("验证失败 (FAIL)")
# --- 演示失败案例 (修改签名) ---
print("\n--- 演示失败案例 (修改签名 r) ---")
is_invalid = sm2_verify(public_key_Q, MESSAGE, USER_ID, r + 1, s)
print(f"修改 r 后的验证: {'FAIL' if not is_invalid else 'PASS'}")
except Exception as e:
print(f"\n发生错误: {e}")
print("请检查 Python 环境是否支持 'sm3' (如安装了 pycryptodome 或使用支持 sm3 的 Python 版本)")代码与 SM 算法的验证流程是一致的,相比于使用 OpenSSL 的库来说可以更加直观地给出整个数学流程和逻辑。
作者:GARFIELDTOM
邮箱:coolerxde@gt.ac.cn